Физики создали самый сложный в мире лабиринт (фото)

Ученые объединили принципы фрактальной геометрии и шахмат, чтобы создать невероятно запутанные лабиринты, описывающие экзотическую форму материи, известную как квазикристаллы. Исследователи, возглавляемые физиком Феликсом Фликером из Бристольского университета в Великобритании, сгенерировали маршруты, называемые гамильтоновыми циклами, в шаблонах, известных как мозаика Аммана-Бенкера.

Эти циклы образуют сложные фрактальные лабиринты, которые, по словам ученых, могут помочь нам лучше понять структуру квазикристаллов. Исследование опубликовано в журнале Physical Review X, пишет ScienceAlert.

Вас также заинтересует: Физики случайно нашли совершенно новый способ записи числа Пи

"Когда мы посмотрели формы линий, которые мы построили, мы заметили, что они образуют невероятно запутанные лабиринты. Размеры последующих лабиринтов растут экспоненциально - и их бесконечное количество", — пояснил физик Фликер. Идея происходит от хода коня на шахматной доске.

Лошадь, прыгая на две ячейки вперед и одну вправо, может посетить каждую ячейку на доске только один раз, прежде чем возвратиться на начальную позицию. Этот маршрут является примером "Гамильтонового цикла" – пути, который проходит через все точки в графе только один раз.

Квазикристаллы – это редкая форма материи, сочетающая в себе упорядоченность и неупорядоченность.

В отличие от обычных кристаллов, где атомы расположены в четкой повторяющейся структуре, атомы в квазикристаллах образуют узор, который не повторяется полностью. Эти узоры сродни апериодическим мозаикам, таким как мозаика Пенроуза или мозаика Амманна-Бенкера, которую использовали ученые.

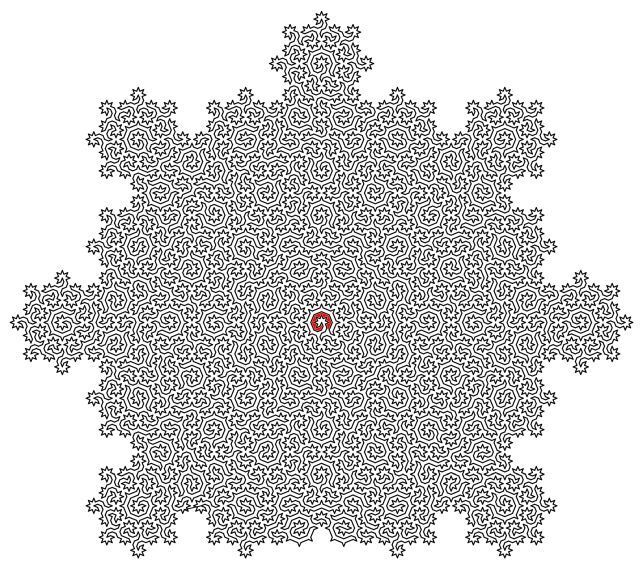
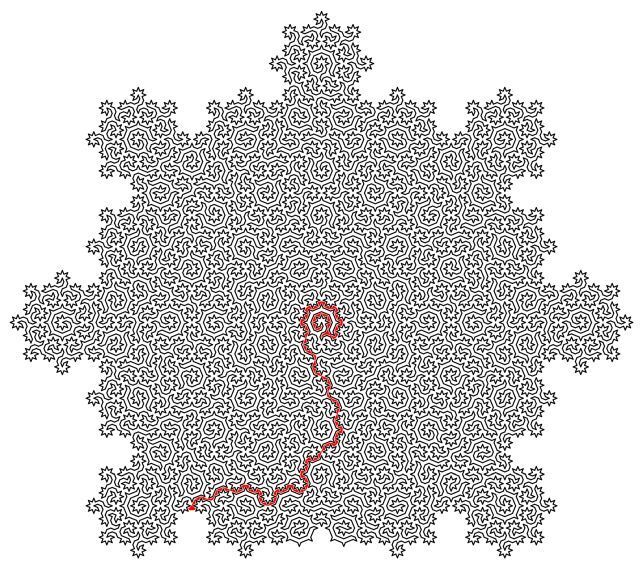
Исследователи использовали мозаику Амманна-Бенкера, чтобы создать гамильтоновые циклы, описывающие структуру квазикристаллов.

Эти циклы проходят через каждый атом в квазикристалле только один раз, соединяя все атомы в одну линию, которая не пересекается сама с собой. Эта линия затем используется для создания лабиринта с исходной точкой и выходом.

Кроме того, исследование может иметь значительные последствия для других сфер, таких как поиск маршрутов, сворачивание белка и захват углерода.

К примеру, нахождение гамильтоновых циклов может помочь решить сложные задачи оптимизации, а квазикристаллы могут быть более эффективными, чем обычные кристаллы, для адсорбции углерода.

Напомним, ученый уверен, что создал уравнение, которое позволит путешествовать по времени.

Хотите получать самые актуальные новости о войне и событиях в Украине – подписывайтесь на наш Telegram-канал!